El método del paralaje es uno de las principales formas de estimar distancias en astronomía. Como se vio en la entrada pasada (Delta Cefei) existe la posibilidad de determinar la distancia a estrellas lejanas, inclusive en otras galaxias usando las estrellas variables Cefeidas, midiendo su periodo y determinando su brillo máximo para saber a que distancia están con respecto a una referencia, es decir con respecto a una estrella Cefeida cuya distancia conozcamos. La pregunta que quedó fue ¿como medir esa distancia a alguna Cefeida sin usar su brillo?
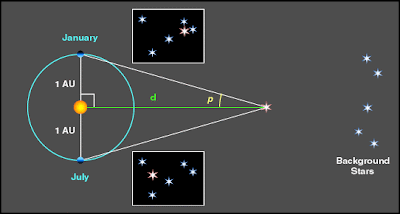
Paralaje. En los recuadros se puede ver la diferencia que se ve al tomar fotografías de la misma estrella desde diferentes puntos, en este caso desde puntos opuestos de la órbita terrestre. En la imagen d es la distancia a la estrella y p el ángulo de paralaje.
La respuesta es el paralaje. Como vimos anteriormente este método consiste en tomar dos fotografías de una estrella, cada una del punto mas alejado posible de donde se tomo la otra. Es el mismo efecto que, al tener nuestro brazo totalmente extendido, causa que uno vea la punta de nuestro dedo contra un fondo un poco diferente al verlo ya sea con el ojo izquierdo o derecho. Fácilmente entendemos que mientras mas separados tengamos los ojos (se recomienda no sacárselos) mayor será la diferencia, y mientras mas largo sea el brazo (mas lejano esté le dedo) menor será la diferencia. La forma de calcular la distancia consiste en medir esta diferencia de posición aparente de una estrella contra el cielo. Pero claro, para ver algo de diferencia o la estrella ha de estar muy cerca (sería como ver el dedo al tener un brazo corto) o la separación entre los lugares desde donde se toman las fotografías están muy separados (lo que sería como tener los ojos muy separados).
Lo ideal es aprovechar el movimiento de la Tierra. Por ejemplo si tomamos una foto de una estrella y 6 meses después, cuando la Tierra se encuentre al extremo opuesto de su órbita, se toma una segunda fotografía de la misma estrella, de esta forma los lugares desde donde se tomaron las fotografías están separados por 2 Unidades Astronómicas, es decir 300 millones de kilómetros. Esta es la máxima distancia que se puede poner entre los lugares de donde se toman dos fotografías sin tener que salir de la Tierra. Bién, digamos que ya tomamos ambas imágenes, ahora se aprovecha una de las primeras lecciones que uno aprende al estudiar matemáticas en secundaria, las relaciones trigonométricas en un triángulo rectángulo. En particular la relación entre el tamaño de los catetos (lados) del triángulo y los ángulos involucrados. Como se ve en la figura siguiente, encontrar la distancia entre Sol y la estrella es el mismo problema que obtener la longitud de lado mas largo del triángulo. Como podrán entender, si se comete un error al medir el ángulo se tendrá también un error en la distancia calculada. Y mientras menor sea el ángulo mas difícil será de medir y mayor el error cometido, por lo que se tiene un cierto límite antes de que el error sea tan grande como para no poder fiarse del paralaje. Pero en cuanto se utilizó este sencillo y confiable método para estimar la distancia a las cefeidas mas cercanas se logró tener toda la información para utilizar a estas estrellas variables como forma de determinar distancias sin tener que medir ángulos por lo que se alcanzan distancias mayores.
Lo ideal es aprovechar el movimiento de la Tierra. Por ejemplo si tomamos una foto de una estrella y 6 meses después, cuando la Tierra se encuentre al extremo opuesto de su órbita, se toma una segunda fotografía de la misma estrella, de esta forma los lugares desde donde se tomaron las fotografías están separados por 2 Unidades Astronómicas, es decir 300 millones de kilómetros. Esta es la máxima distancia que se puede poner entre los lugares de donde se toman dos fotografías sin tener que salir de la Tierra. Bién, digamos que ya tomamos ambas imágenes, ahora se aprovecha una de las primeras lecciones que uno aprende al estudiar matemáticas en secundaria, las relaciones trigonométricas en un triángulo rectángulo. En particular la relación entre el tamaño de los catetos (lados) del triángulo y los ángulos involucrados. Como se ve en la figura siguiente, encontrar la distancia entre Sol y la estrella es el mismo problema que obtener la longitud de lado mas largo del triángulo. Como podrán entender, si se comete un error al medir el ángulo se tendrá también un error en la distancia calculada. Y mientras menor sea el ángulo mas difícil será de medir y mayor el error cometido, por lo que se tiene un cierto límite antes de que el error sea tan grande como para no poder fiarse del paralaje. Pero en cuanto se utilizó este sencillo y confiable método para estimar la distancia a las cefeidas mas cercanas se logró tener toda la información para utilizar a estas estrellas variables como forma de determinar distancias sin tener que medir ángulos por lo que se alcanzan distancias mayores.
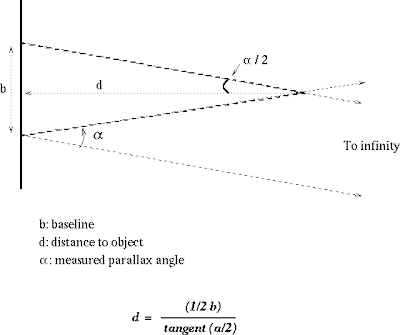
Forma de calcular la distancia usando el ángulo de paralaje (en este caso se designa con la letra alfa).
El descubrimiento de Leavitt permitió darnos cuenta de lo realmente grande que es el universo. Digamos que Leavitt expandió nuestro universo, al pasar el tener el tamaño de la Vía Láctea hasta abarcar todo el grupo local.
No hay comentarios:
Publicar un comentario
Hola, sus comentarios y preguntas siempre son bienvenidos. Les agradecería si incluyen su nombre (o un "nick" cualquiera) para hacer la interacción mas amena. Pueden poner el nombre que deseen usando la penúltima opción de "Comentar como:"